





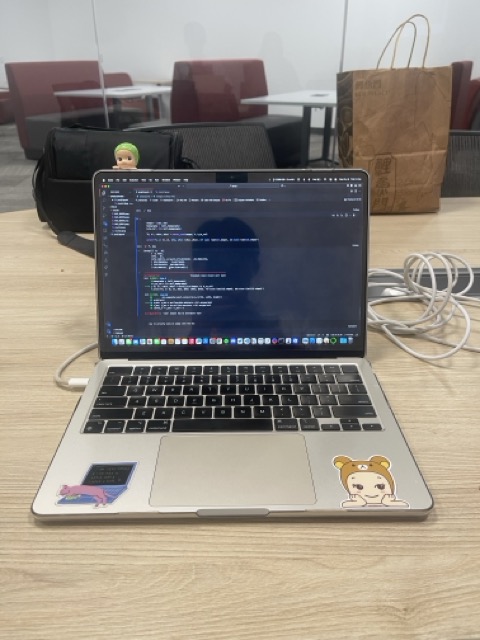

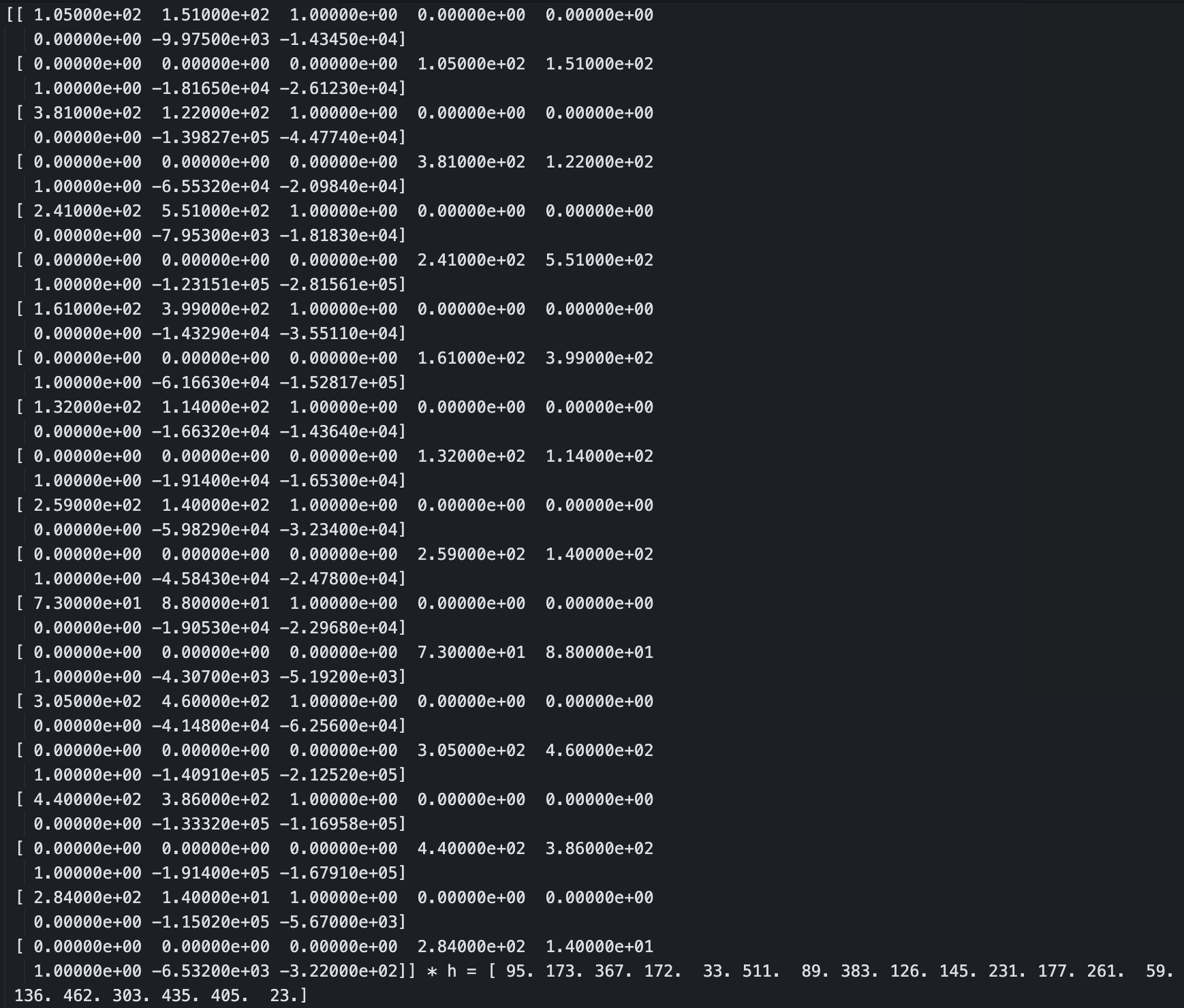
In this part, I implemented computeH to find the projective transformation (homography) between two sets of corresponding points. I built a system of equations using the point correspondences and solved for the homography matrix H that satisfies p′ = Hp (or Ah = b), and then scaled it with W to get the homogeneous coordinates. I tested my results against OpenCV’s cv2.findHomography() to see how close my H was. It turned out to be pretty close!
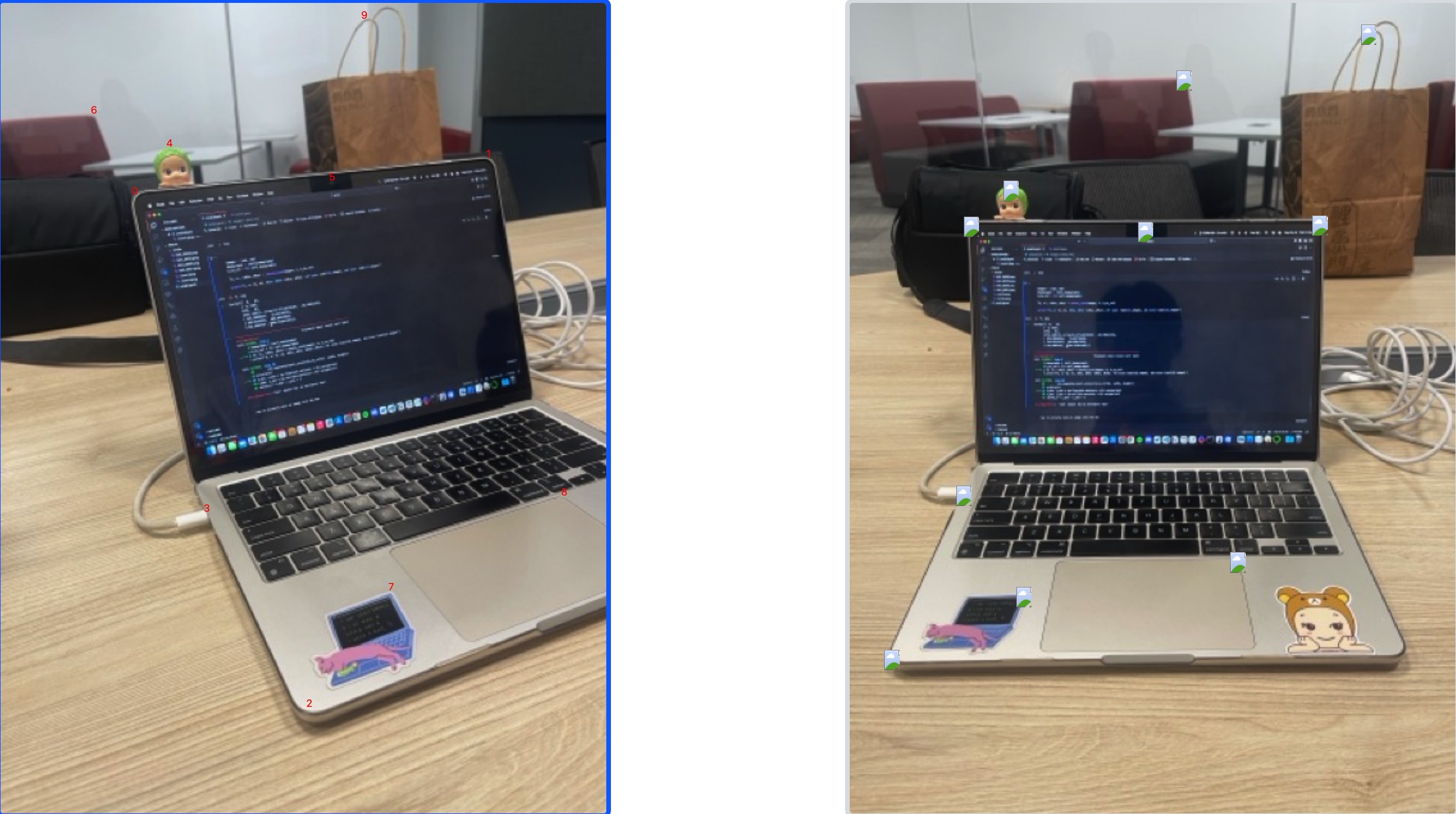

Using the computed homography, we implemented warp_onto_ref with two modes (nearest neighbor) and (bilinear) from scratch to perform inverse warping. For each pixel in the output image, we mapped it back to the source image using H^-1, then sampled its color by rounding to nearest pixel (nearest neighbor), or interpolating from the four surrounding pixels (bilinear). This allows us to get our image in terms of our reference image's perspective.


Finally, I created a panoramic mosaic by aligning multiple images into a single canvas. I computed homographies from each image to a common reference frame, determined the overall bounding box, and placed all images onto a shared canvas using our warping functions. I created alpha masks to try to blend overlapping regions smoothly, but wasn't able to get it to work before the part 1 deadline. The final result is a visually seamless panorama showing all images correctly aligned, albeit a little bit blurry.






Many of these pictures were done in a hurry, kind of like a proof of concept that my functions worked for the part 1 deadlone. I hope to redo this part and use better images within the next few days to hopefully get better looking results, but I hope this is enough for full credit for part 1 as of now. Thank you!